Find a Transition State

Let's now attempt to find a transition state for formaldehyde, say moving one of the hydrogens onto the oxygen. We will define the two states, then calculate the force at various intervals along the way. The transition state will be where the energy is a maximum and the force is zero along the transition axis. Sounds good, but how is this done in PAW? We do this by setting constraints on the system in our STRC file. For example, we can restrict the hydrogen mentioned to a plane, and then move that plane slowly toward the desired position. Let's give it a try.

1.

Edit the h2co.strc file to describe our new dynamic system

• We will use the !CONSTRAINTS!MIDPLANE block to describe our desired constraint (See Figure 14.
• The TRANSLATION block is applied to the 'ALL' group by default, so above, we are preventing the molecular system from running away from us in translational space.
• ATOM1 and ATOM3 define the vector normal to our constraint plane and ATOM2 is the atom that is to be restricted.
• MOVE says that we want to change the value of the constraint to a new VALUE, which in this case is x in the location where the plane is attached to the vector, e.g. at point R₁ + x(R₃ - R₁). By moving this attachment point, we move the plane from ATOM1 when x=0 to ATOM3 when x=1. Let's begin with x=0.5.
• NSTEP is the number of steps we want to take to get to the new constraint value. Please note that if we don't give it enough steps, we will be moving too fast to get an accurate description of what is happening, as in most AIMD calculations.
• Setting SHOW to .true (boolean values can be entered as T,F or .true,.false) will print out some extra information into the constraint report, h2co_constr.report, file. In particular, we are looking for the value and force of the constraint so that we can watch the dynamics by monitoring this output.

  

Figure: h2co.strc (3)

2.

Edit the .cntl file (h2co.cntl_6)

• Turn off the wave analysis
• Change the upper RDYN friction to 0.001 and make sure all scale factors are unity.

3.

Run the calculation: paw_run -c h2co.cntl

4.

Observe the output

• It will probably print out some info to the stdout mentioning deviation from the constraint. Don't worry about this unless the values look really extreme. It is really just debugging information.
• Look at the .prot file to get an idea of how the total energy is changing. We should see it going up as the movement of the hydrogen occurs (because we are making it do something it doesn't necessarily want to do). The temperature should go up, too.
• Now, look at the h2co_constr.report file. It will print out the following info at each timestep: (x force), where x is our constraint value and force is the force on that constraint. We should see the force increase in the opposite direction as x goes toward 0.5.
• We can visualize this in a better way if we plot both the constraint and the force vs the number of timesteps (to do this I had to use awk and emacs to format the output so xmgr was happy). This shows us that we are not yet at the right transition state because the force is not yet zero. paw_show -e also elucidates that we are not yet at an energy maximum.

5.

Getting warmer . . . (h2co.strc_3)

• Looks like we need to go a little bit further. Edit the .strc file, change the value of the constraint from 0.5 to 0.7, and change the number of steps to 150 (because we are not going as far). Save the file.
• Aside . . . At this point I decided to make life a little easier on myself by writing a little script to run the calculation, rather than having to remember what to type in each time. Basically create a h2co.doit file and include the command you want in that file. Make the file executable (chmod u+x h2co.doit) and now all we have to do is type ``h2co.doit'' to run the calculation. Neat, huh? . . . end of Aside.
• Re-run the calculation.
• Plot the energy, and see that it has passed a maximum during our transition.
• Plot the constraint and the force vs. number of timesteps, shown in Figure 15, and see that the force crosses zero when the constraint is about 0.6. Looks like we have a winner!
  
    

  Figure: Notice the spikes that result from our sudden starting and stopping, such that we briefly lose the electrons. Nifty!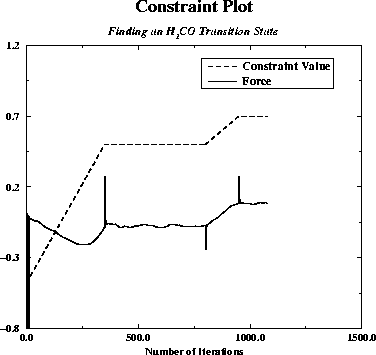

  
  
  
• Now we want to go back to 0.6 slowly and then let it relax so we can see what it looks like. Change the constraint to 0.6 and re-run it.

6.

Letting it Relax (ahhhh)

• Notice that we gave the hydrogen 350 timesteps to reach its destination, and we ran a total of 500 timesteps. This is to give it a little time to relax, but paw_show -e elucidates that we should give it a bit more time, perhaps with an appropriate change to the friction.