Transition State Search Algorithms: Ridge and cNEB Methods

 

 

  1. Transition States
  2. Basic – Drag Method
  3. The Ridge Method
  4. The Climbing Image Method
  5. Approach

Transition State Searching

Initial State à MEP à Final State

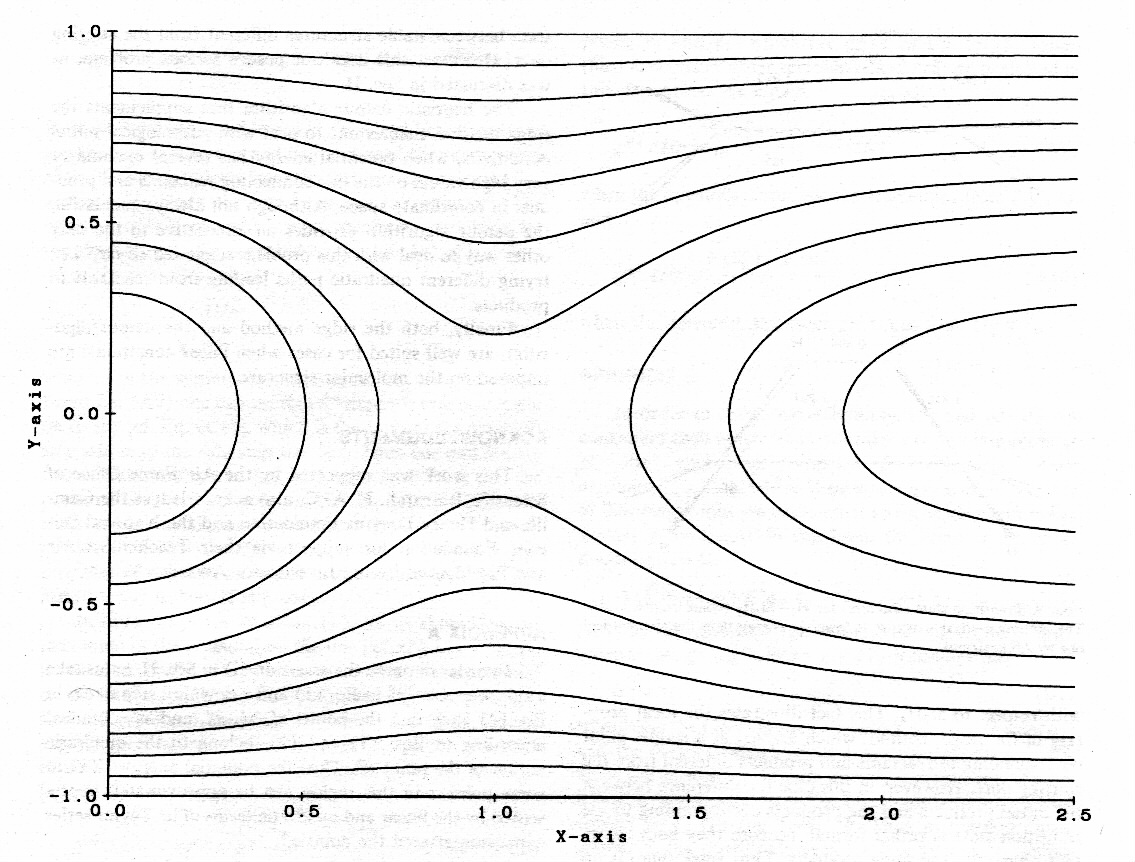
MEP = minimum energy path, which can have several maxima and minima

Why search for transition states?

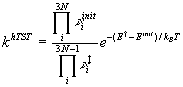
Search Algorithms - Basic

The Drag Method:

Fix a drag coordinate, and relax all other degrees of freedom to minimize total E.

Then, follow drag coordinate and drag from R to P.

Inverted force determines propagation direction.

Problem: selected drag coordinate may not lead to saddle point.

Better Search Algorithms

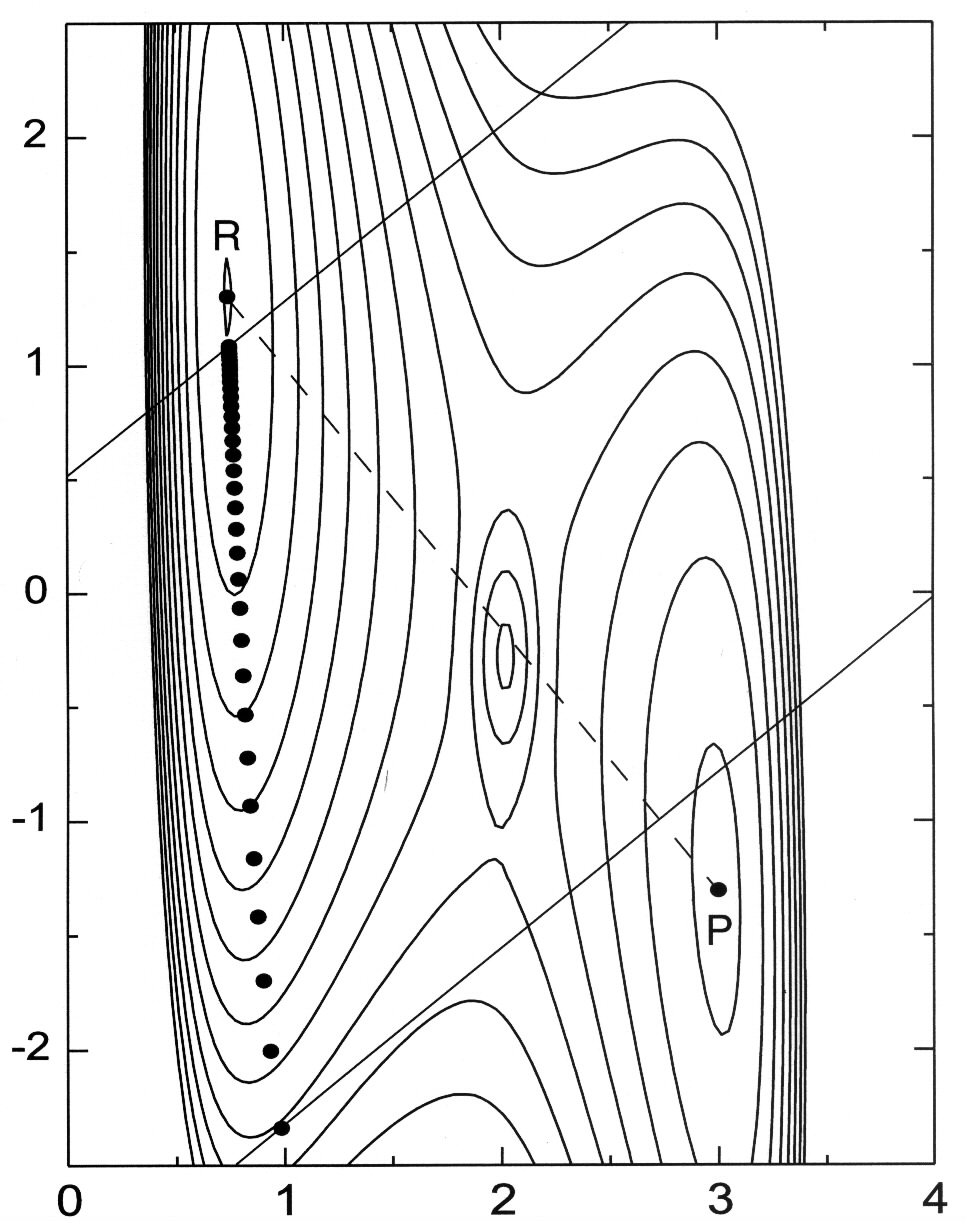
The Ridge Method:

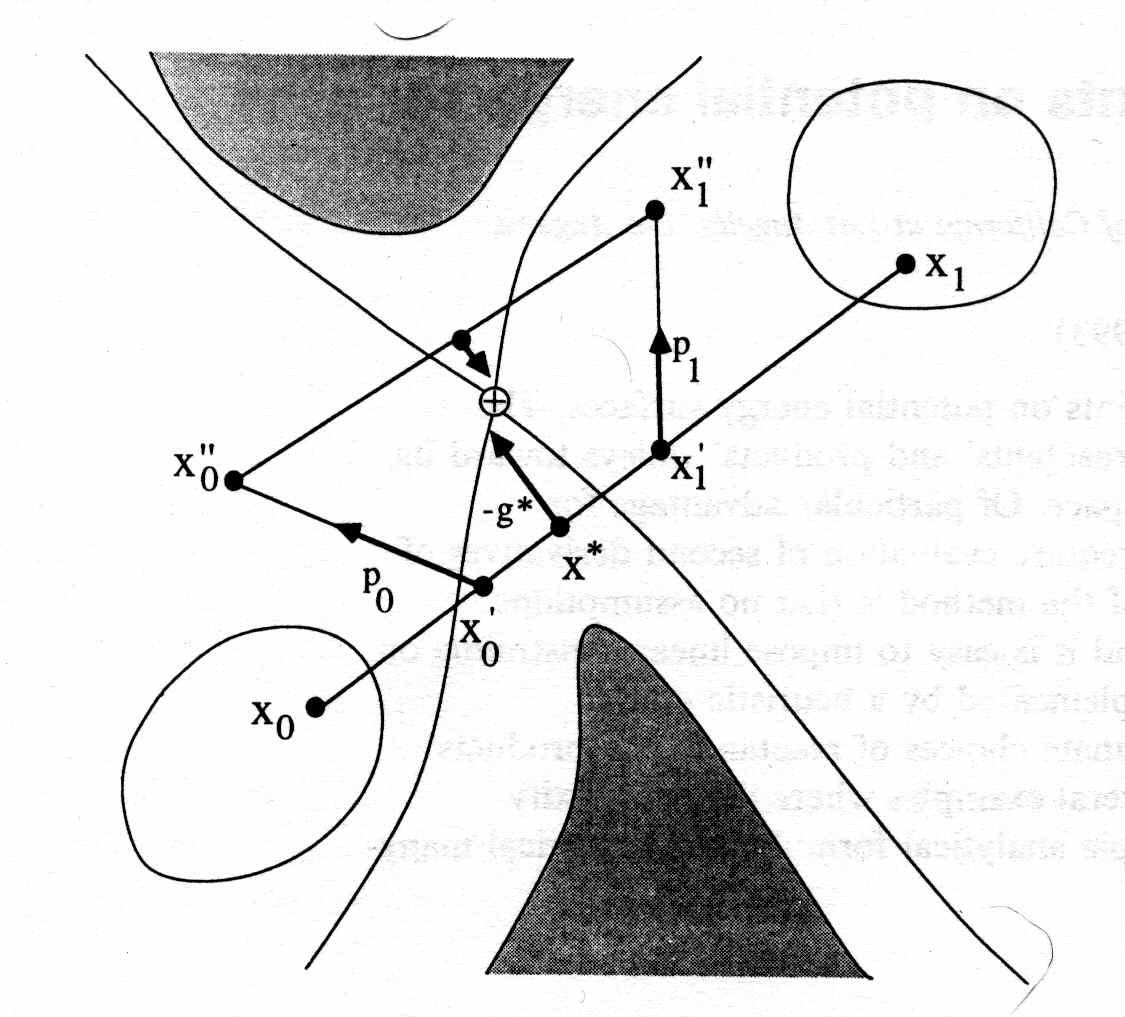Interval:

downhill steps:

check for max on:

and check that it’s

Then, repeat until gradient at x* is sufficiently small.

Problems: converges quickly to saddle point vicinity, but steps get smaller as we get closer, and halts or requires many iterations to reach high tolerance.

 

Other Search Algorithms

Nudged Elastic Band (NEB):

Spring-connected images form the R-P pathway.

Minimize an object:

But images tend to cut corners and slide downhill, so ‘nudge’:

For each image: calculate E, gradients, tangent; nudge w/force projection, minimize the system

Problems: saddle point needs to be estimated from images

Climbing Image NEB (cNEB):

Highest-energy image climbs up to the saddle point.

How it’s done:

 

The highest-energy image then converges to the saddle point, and no interpolation is required.

Also, the MEP is obtained without extra effort.

 

Approach

Observations:

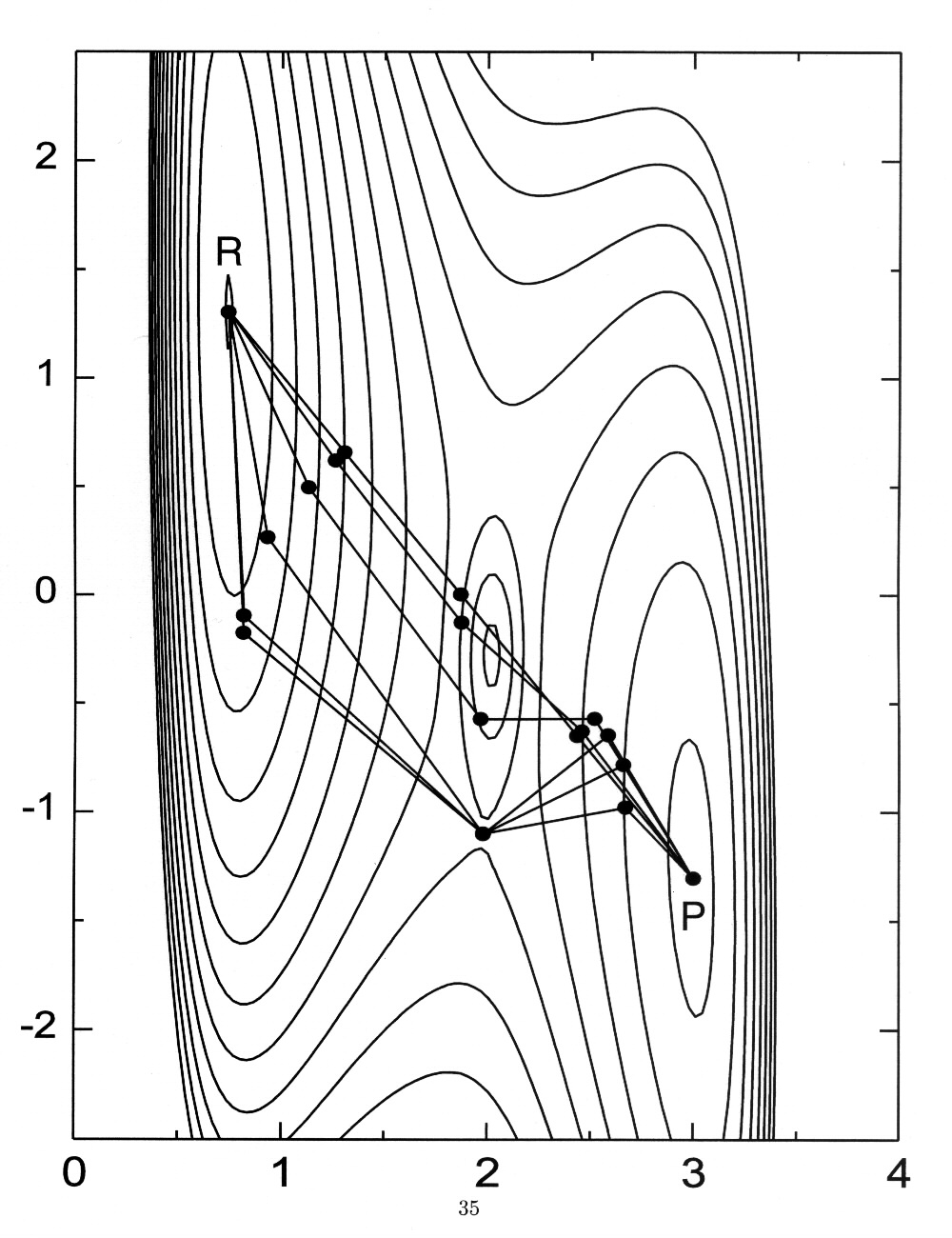
Computational effort (# of force evaluations) for Ridge is lower for low convergence tolerance, but increases rapidly for higher tolerance.

cNEB does not suffer this problem as much.

Implementation:

Start with Ridge à switch to cNEB

Both codes only require the energies and the gradients to proceed (not the Hessian), so can be implemented within the same DFT code (VASP).

Efforts:

Benchmark each code separately.

Find an optimal switching tolerance or code-in a self-tuning one.