prob2.html

>

> with(linalg):
with(plots):

First, we develop the FWT for the Haar wavelet

>    H8 := evalm( 1/2 * matrix(8,8,[
1, 0, 0, 0, 1, 0, 0, 0,
1, 0, 0, 0, -1, 0, 0, 0,
0, 1, 0, 0, 0, 1, 0, 0,
0, 1, 0, 0, 0,-1, 0, 0,
0, 0, 1, 0, 0, 0, 1, 0,
0, 0, 1, 0, 0, 0,-1, 0,
0, 0, 0, 1, 0, 0, 0, 1,
0, 0, 0, 1, 0, 0, 0,-1]));

H4 := diag(
evalm(1/2 *
matrix(4,4,[ 1, 0, 1, 0,
             1, 0, -1, 0,
             0, 1, 0, 1,
             0, 1, 0,-1])),
diag(1$4));

H2 := diag(
evalm(1/2 *
matrix(2,2,[1, 1,
            1, -1])),
diag(1$6));

> Haar_Wavelet_Transform := evalm( H8 &* H4 &* H2 );

>

Now:
do the same analysis for My Wavelet from Problem 1

>    alias( h0 = (1+sqrt(10))/4 );
alias( h1 = (1/2+sqrt(10))/4 );
alias( h2 = (1-sqrt(10))/4 );
alias( h3 = (1/2-sqrt(10))/4 );

T8 := evalm( 1/sqrt(2) * matrix(8,8,[
h0, h1, h2, h3,   0,   0,   0,   0,
0,   0, h0, h1, h2, h3,   0,   0,
0,   0,   0,   0, h0, h1, h2, h3,
h2, h3,   0,   0,   0,   0, h0, h1,
h3, -h2, h1, -h0,   0,   0,   0,   0,
0,   0, h3, -h2, h1, -h0,   0,   0,
0,   0,   0,   0, h3, -h2, h1, -h0,
h1, -h0,   0,   0,   0,   0, h3, -h2
]));

T4 := diag(
evalm(1/sqrt(2) *
matrix(4,4,[ h0, h1, h2, h3,
             h2, h3, h0, h1,
          h3, -h2, h1, -h0,
             h1, -h0, h3, -h2])),
diag(1$4));

T2 := diag(
evalm(1/sqrt(2) *
matrix(2,2,[h0+h2, h1+h3,
            h3+h1,-h0-h2])),
diag(1$6));

> # W8 is the discrete Wavelet transform matrix

W8 := simplify(evalm( T2 &* T4 &* T8 ));

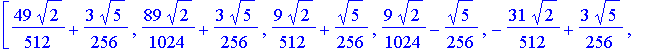
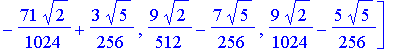
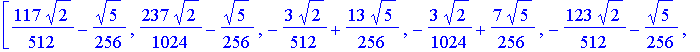
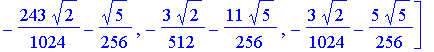
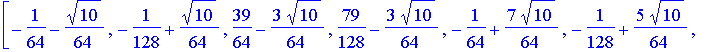
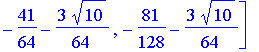
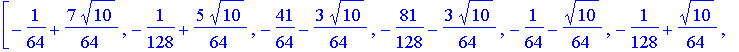
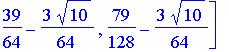
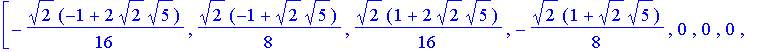
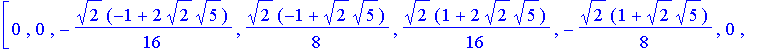
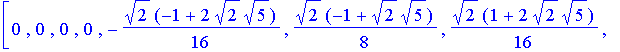
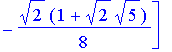
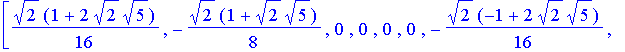
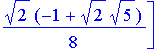
> v1 := [1,0,0,0, 0,0,0,0];
Hx := evalm( Haar_Wavelet_Transform &* v1 ):
matrix(8,1, (i,j) -> Hx[i] );

> Wx := evalm( W8 &* v1 ):
matrix(8,1, (i,j) -> Wx[i] );

> v2 := [1,1,1,1, 1,1,1,1];
Hx := evalm( Haar_Wavelet_Transform &* v2 ):
matrix(8,1, (i,j) -> Hx[i] );
Wx := evalm( W8 &* v2 ):
matrix(8,1, (i,j) -> Wx[i] );

> v3 := [1,-1,1,-1, 1,-1,1,-1];
Hx := evalm( Haar_Wavelet_Transform &* v3 ):
matrix(8,1, (i,j) -> Hx[i] );
Wx := evalm( W8 &* v3 ):
matrix(8,1, (i,j) -> Wx[i] );

> v4 := [1,1,1,1, -1,-1,-1,-1];
Hx := evalm( Haar_Wavelet_Transform &* v4 ):
matrix(8,1, (i,j) -> Hx[i] );
Wx := evalm( W8 &* v4 ):
matrix(8,1, (i,j) -> Wx[i] );

>